📘 त्रिभुज - अभ्यास प्रश्न
ये प्रश्न परीक्षा की दृष्टि से अत्यंत महत्वपूर्ण हैं, जिन्हें हर विद्यार्थी को जरूर तैयार करना चाहिए ✅
प्र.1: कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए:
(i) सभी वृत्त ............. होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग ............. होते हैं। (समरूप, सर्वांगसम)
(iii) सभी ............. त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि
(a) उनके संगत कोण ............. हों तथा
(b) उनकी संगत ............. भुजाएँ हों। (बराबर, समानुपाती)
उत्तर:
(i) समरूप
(ii) समरूप
(iii) समबाहु
(iv) (a) बराबर, (b) समानुपाती
प्र.2: निम्नलिखित युग्मों के दो-दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं
उत्तर:
(i) समरूप आकृतियाँ:
(a) दो समबाहु त्रिभुज
(b) दो वर्ग
(ii) समरूप नहीं होने वाली आकृतियाँ:
(a) एक वृत्त और एक त्रिभुज
(b) एक समद्विबाहु त्रिभुज और एक विषमबाहु त्रिभुज
प्र.1: आकृति 6.17 (i) और (ii) में, DE ∥ BC है। (i) में EC और (ii) में AD ज्ञात कीजिए:
हल:
(i) ∆ABC में:
DE ∥ BC
(by Basic Proportionality Theorem~ थेल्स प्रमेय)
⇒ AD / DB = AE / EC
मान लीजिए EC = x
⇒ 1.5/3 = 1 / x
✍ 1.5x = 1 × 3
⇒ x = 3/1.5
⇒ x = 2 ⇒ x = 2 cm ✅
अतः AD = 2 cm
(ii) ∆ABC में:
DE ∥ BC
(by Basic Proportionality Theorem~ थेल्स प्रमेय)
⇒ AD / DB = AE / EC
मान लीजिए AD = x
⇒ x/7.2 = 1.8 / 5.4
✍ x = 1.8 × 7.2 / 5.4
⇒ x = 2.4
⇒ x = 2.4 ⇒ x = 2.4 cm ✅
अतः AD = 2.4 cm
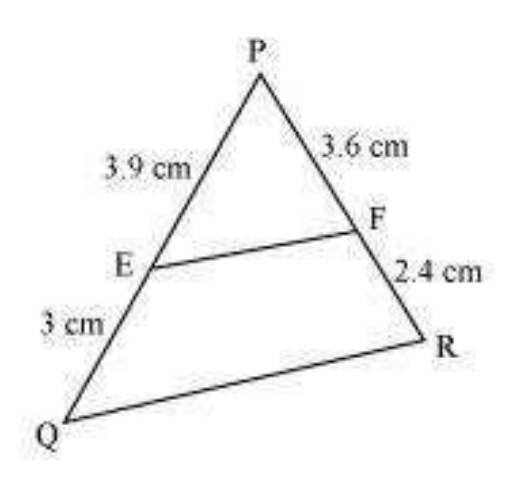
प्र.2: किसी ΔPQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। दिए गए स्थितियों के लिए जाँचिए कि क्या EF ∥ QR है:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm
PE/EQ = 3.9/3 = 1.3, PF/FR = 3.6/2.4 = 1.5
∵ 1.3 ≠ 1.5 ⇒ EF ∦ QR ❌
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm
PE/QE = 4/4.5 = 8/9, PF/RF = 8/9
∴ दोनों अनुपात बराबर हैं
⇒ EF ∥ QR ✅
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm
PE/PQ = 0.18/1.28 = 9/64
PF/PR = 0.36/2.56 = 9/64
∴ दोनों अनुपात बराबर हैं
⇒ EF ∥ QR ✅
प्र.3: आकृति 6.18 में यदि LM ∥ CB और LN ∥ CD हो तो सिद्ध कीजिए कि:
AM / AB = AN / AD
हल:
∵ ΔABC में
LM ∥ CB (दिया है)
(Basic Proportionality Theorem से )
⇒ AM / MB = AL / LC …(1)
∵ ΔADC में
LN ∥ CD (दिया है)
(थेल्स प्रमेय से)
⇒ AN / ND = AL / LC …(2)
अब (1) और (2) से:
AM / MB = AL / AC = AN / ND
⇒ AM / MB = AN / ND
अब पलटने पर,
MB / AM = ND / AN
⇒ (MB / AM) + 1 = (ND / AN) + 1
⇒ (MB + AM) / AM + (ND + AN)/ AN
⇒ AB/AM = AD/AN proved.
प्र.4: आकृति 6.19 में यदि AC ∥ DF और AE ∥ DB है तो सिद्ध कीजिए कि:
BF / FE = EC / CD
हल:
△ABC में, दिया गया है कि DE ∥ AC
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार, हमें मिलता है:
∴ BD / DA = BE / EC ………………………………………………(i)
△BAE में, दिया गया है कि DF ∥ AE
अतः आधार समानुपातिता प्रमेय के अनुसार, हमें मिलता है:
∴ BD / DA = BF / FE ………………………………………………(ii)
समीकरण (i) और (ii) से, हमें मिलता है:
∴ BE / EC = BF / FE
अतः सिद्ध हुआ कि:
BE / EC = BF / FE
प्र.5: आकृति 6.20 में DE ∥ OQ और DF ∥ OR है। दर्शाइए कि EF ∥ QR है।
हल:
दिया गया है,
△PQO में, DE ∥ OQ
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार:
∴ PD / DO = PE / EQ …………………………(i)
फिर, △POR में दिया गया है कि DF ∥ OR
अतः आधार समानुपातिता प्रमेय के अनुसार:
∴ PD / DO = PF / FR …………………………(ii)
समीकरण (i) और (ii) से प्राप्त होता है:
∴ PE / EQ = PF / FR
अतः आधार समानुपातिता प्रमेय के व्युत्क्रम (Converse of BPT) के अनुसार:
EF ∥ QR, △PQR में
प्र.6: आकृति 6.21 में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB ∥ PQ और AC ∥ PR है। दर्शाइए कि BC ∥ QR।
हल:
यहाँ दिया गया है,
△OPQ में, AB ∥ PQ
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार:
∴ OA / AP = OB / BQ ……………(i)
साथ ही दिया गया है,
△OPR में, AC ∥ PR
अतः आधार समानुपातिता प्रमेय के अनुसार:
∴ OA / AP = OC / CR ……………(ii)
समीकरण (i) और (ii) से हमें प्राप्त होता है:
∴ OB / BQ = OC / CR
अतः आधार समानुपातिता प्रमेय के व्युत्क्रम (Converse of BPT) के अनुसार:
△OQR में, BC ∥ QR
प्र.7: प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
हल:
दिया गया है, △ABC में D, AB का मध्यबिंदु है, अर्थात AD = DB
एक रेखा जो BC के समानांतर है, वह AC को E पर प्रतिछेद करती है, जैसा कि चित्र में दिखाया गया है, अर्थात DE ∥ BC
हमें सिद्ध करना है कि E, AC का मध्यबिंदु है।
चूंकि D, AB का मध्यबिंदु है,
∴ AD = DB
⇒ AD / DB = 1 …………………………. (i)
△ABC में, DE ∥ BC
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार:
AD / DB = AE / EC
समीकरण (i) से,
⇒ 1 = AE / EC
∴ AE = EC
अतः सिद्ध हुआ कि:
E, AC का मध्यबिंदु है।
प्र.8: प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है।
हल:
दिया गया है, △ABC में D और E क्रमशः AB और AC के मध्यबिंदु हैं, अर्थात
AD = DB और AE = EC
हमें सिद्ध करना है: DE ∥ BC
चूंकि D, AB का मध्यबिंदु है,
∴ AD = DB
⇒ AD / DB = 1 ……………………………… (i)
साथ ही दिया गया है, E, AC का मध्यबिंदु है,
∴ AE = EC
⇒ AE / EC = 1 ……………………………… (ii)
समीकरण (i) और (ii) से हमें प्राप्त होता है:
AD / DB = AE / EC
अब, आधार समानुपातिता प्रमेय के व्युत्क्रम (Converse of Basic Proportionality Theorem) के अनुसार:
DE ∥ BC
अतः सिद्ध हुआ कि:
DE ∥ BC
प्र.9: ABCD एक समांतर चतुर्भुज है जिसमें AB ∥ DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि AO/BO = CO/DO।
हल:
दिया गया है, ABCD एक समलंब (trapezium) है जिसमें AB ∥ DC है तथा विकर्ण AC और BD एक-दूसरे को O बिंदु पर प्रतिच्छेद करते हैं।
हमें सिद्ध करना है: AO / BO = CO / DO
बिंदु O से एक रेखा EO खींचते हैं, जो AD को E बिंदु पर स्पर्श करती है, इस प्रकार कि:
EO ∥ DC ∥ AB
अब, △ADC में, EO ∥ DC
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार:
AE / ED = AO / CO ……………..(i)
अब, △ABD में, EO ∥ AB
अतः आधार समानुपातिता प्रमेय के अनुसार:
DE / EA = DO / BO ……………..(ii)
समीकरण (i) और (ii) से हमें प्राप्त होता है:
AO / CO = BO / DO
⇒ AO / BO = CO / DO
अतः सिद्ध हुआ कि:
AO / BO = CO / DO
प्र.10: ABCD एक समांतर चतुर्भुज है जिसमें AB ∥ DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि AO/BO = CO/DO।
हल:
दिया गया है, चतुर्भुज ABCD जिसमें विकर्ण AC और BD एक-दूसरे को O बिंदु पर प्रतिच्छेद करते हैं और
AO / BO = CO / DO
हमें सिद्ध करना है: ABCD एक समलंब (trapezium) है।
बिंदु O से एक रेखा EO खींचते हैं जो AD को E पर स्पर्श करती है, इस प्रकार कि:
EO ∥ DC ∥ AB
अब, △DAB में EO ∥ AB
अतः आधार समानुपातिता प्रमेय (Basic Proportionality Theorem) के अनुसार:
DE / EA = DO / OB ……………………… (i)
साथ ही दिया गया है:
AO / BO = CO / DO
⇒ AO / CO = BO / DO
⇒ CO / AO = DO / BO
⇒ DO / OB = CO / AO ……………………… (ii)
समीकरण (i) और (ii) से हमें प्राप्त होता है:
DE / EA = CO / AO
अब, आधार समानुपातिता प्रमेय के व्युत्क्रम (Converse of Basic Proportionality Theorem) के अनुसार:
EO ∥ DC
और EO ∥ AB भी दिया गया है
⇒ AB ∥ DC
अतः सिद्ध हुआ कि:
ABCD एक समलंब (trapezium) है जिसमें AB ∥ DC।
प्र.1: बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता की कसौटी को लिखिए तथा समरूप त्रिभुजों को संकेतात्मक रूप में व्यवस्थित कीजिए।
हल:
(i) दिया गया है, △ABC और △PQR में:
∠A = ∠P = 60°
∠B = ∠Q = 80°
∠C = ∠R = 40°
अतः AAA समरूपता कसौटी के अनुसार:
∴ △ABC ~ △PQR
(ii) दिया गया है, △ABC और △PQR में:
AB / QR = 2 / 4 = 1 / 2
BC / RP = 2.5 / 5 = 1 / 2
CA / PA = 3 / 6 = 1 / 2
अतः SSS समरूपता कसौटी के अनुसार:
∴ △ABC ~ △QRP
(iii) दिया गया है, △LMP और △DEF में:
LM = 2.7, MP = 2, LP = 3
EF = 5, DE = 4, DF = 6
MP / DE = 2 / 4 = 1 / 2
PL / DF = 3 / 6 = 1 / 2
LM / EF = 2.7 / 5 = 27 / 50
यहाँ, MP / DE = PL / DF ≠ LM / EF
अतः △LMP और △DEF समरूप नहीं हैं।
(iv) दिया गया है, △MNL और △QPR में:
MN / QP = ML / QR = 1 / 2
∠M = ∠Q = 70°
अतः SAS समरूपता कसौटी के अनुसार:
∴ △MNL ~ △QPR
(v) दिया गया है, △ABC और △DEF में:
AB = 2.5, BC = 3, ∠A = 80°
EF = 6, DF = 5, ∠F = 80°
AB / DF = 2.5 / 5 = 1 / 2
BC / EF = 3 / 6 = 1 / 2
लेकिन ∠B ≠ ∠F
अतः △ABC और △DEF समरूप नहीं हैं।
(vi) △DEF में,
त्रिभुजों के कोणों का योग = 180°
∠D + ∠E + ∠F = 180°
⇒ 70° + 80° + ∠F = 180°
⇒ ∠F = 30°
इसी प्रकार, △PQR में:
∠P + 80° + 30° = 180°
⇒ ∠P = 70°
अब, दोनों त्रिभुजों की तुलना करें:
∠D = ∠P = 70°
∠E = ∠Q = 80°
∠F = ∠R = 30°
अतः AAA समरूपता कसौटी के अनुसार:
∴ △DEF ~ △PQR
प्र.2: आकृति 6.35 में, △ODC ∼ △OBA है। ∠BOC = 125° तथा ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
हल:
जैसा कि चित्र से स्पष्ट है, DOB एक सीधी रेखा है।
अतः ∠DOC + ∠COB = 180°
⇒ ∠DOC = 180° – 125° (दिया गया है ∠BOC = 125°)
⇒ ∠DOC = 55°
अब, △DOC में, त्रिभुज के कोणों का योग 180° होता है:
∠DCO + ∠CDO + ∠DOC = 180°
⇒ ∠DCO + 70° + 55° = 180° (दिया गया है ∠CDO = 70°)
⇒ ∠DCO = 55°
दिया गया है कि △ODC ~ △OBA
अतः समरूप त्रिभुजों में संगत कोण समान होते हैं:
⇒ ∠OAB = ∠OCD
⇒ ∠OAB = 55°
अतः सिद्ध हुआ कि:
∠OAB = 55°
प्र.3: समांतर चतुर्भुज ABCD में, AB ∥ DC है। विकर्ण AC और BD बिंदु O पर प्रतिच्छेद करते हैं। दो त्रिभुजों की समरूपता की कसौटी का प्रयोग करते हुए, दर्शाइए कि
OA / OC = OB / OD।
हल:
△DOC और △BOA में,
चूंकि AB ∥ CD है, अतः परस्पर अंतःकोण (alternate interior angles) बराबर होंगे:
∴ ∠CDO = ∠ABO
उसी प्रकार,
∠DCO = ∠BAO
साथ ही, दोनों त्रिभुजों △DOC और △BOA में,
विपरीत कोण (vertically opposite angles) समान होते हैं:
∴ ∠DOC = ∠BOA
अतः, AAA समरूपता की कसौटी के अनुसार:
∴ △DOC ~ △BOA
इसलिए समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होंगी:
DO / BO = OC / OA
⇒ OA / OC = OB / OD
अतः सिद्ध हुआ कि:
OA / OC = OB / OD
प्र.4: आकृति 6.36 में,
यदि QR/QS = QT/PR तथा ∠1 = ∠2 है,
तो दर्शाइए कि △PQS ∼ △TQR है।
हल:
△PQR में,
दिया गया है: ∠PQR = ∠PRQ
∴ PQ = PR ……………………… (i)
दिया गया है:
QR / QS = QT / PR
समीकरण (i) का उपयोग करते हुए,
⇒ QR / QS = QT / QP ……………………… (ii)
अब, △PQS और △TQR में:
QR / QS = QT / QP (समीकरण (ii) से)
और ∠Q = ∠Q (साझा कोण)
∴ △PQS ~ △TQR [SAS समरूपता की कसौटी द्वारा]
प्र.5: एक त्रिभुज △PQR की भुजाएं PR और QR हैं। बिंदु S, PR पर तथा T, QR पर स्थित हैं।
यदि ∠P = ∠RTS, तो सिद्ध कीजिए कि △RPQ ∼ △RTS।
हल:
दिया गया है: S और T, △PQR की भुजाओं PR और QR पर स्थित बिंदु हैं।
और ∠P = ∠RTS
अब, त्रिभुज △RPQ और △RTS में:
∠RTS = ∠QPS (दिया गया है)
∠R = ∠R (साझा कोण)
अतः AA समरूपता कसौटी के अनुसार:
∴ △RPQ ~ △RTS
प्र.6: आकृति 6.37 में, यदि △ABE ≅ △ACD है, तो दर्शाइए कि
i) ABE ≅ ACD से क्या निष्कर्ष निकलता है।
हल:
दिया गया है: △ABE ≅ △ACD
∴ AB = AC [CPCT के अनुसार] ……………………………….(i)
और, AD = AE [CPCT के अनुसार] ……………………………(ii)
अब, △ADE और △ABC में:
समीकरण (ii) को (i) से विभाजित करते हैं:
AD / AB = AE / AC
साथ ही, ∠A = ∠A (साझा कोण)
अतः SAS समरूपता की कसौटी के अनुसार:
∴ △ADE ~ △ABC
प्र.7: आकृति 6.38 में, △ABC के भीतर AD और CE रेखाएं इस प्रकार खींची गई हैं कि वे O पर प्रतिच्छेद करती हैं। दर्शाइए कि:
हल:
दिया गया है कि △ABC की ऊँचाइयाँ AD और CE एक-दूसरे को बिंदु P पर प्रतिच्छेद करती हैं।
(i) △AEP और △CDP में:
∠AEP = ∠CDP = 90° (प्रत्येक त्रिभुज की ऊँचाई होने के कारण)
∠APE = ∠CPD (विपरीत कोण — Vertically opposite angles)
अतः AA समरूपता कसौटी के अनुसार:
∴ △AEP ~ △CDP
(ii) △ABD और △CBE में:
∠ADB = ∠CEB = 90° (प्रत्येक ऊँचाई पर आधारित)
∠ABD = ∠CBE (साझा कोण)
अतः AA समरूपता कसौटी के अनुसार:
∴ △ABD ~ △CBE
(iii) △AEP और △ADB में:
∠AEP = ∠ADB = 90°
∠PAE = ∠DAB (साझा कोण)
अतः AA समरूपता कसौटी के अनुसार:
∴ △AEP ~ △ADB
(iv) △PDC और △BEC में:
∠PDC = ∠BEC = 90°
∠PCD = ∠BCE (साझा कोण)
अतः AA समरूपता कसौटी के अनुसार:
∴ △PDC ~ △BEC
प्र.8: समांतर चतुर्भुज ABCD को बढ़ाई गई भुजा AD पर स्थित E एवं BE को बढ़ाकर F पर प्रतिच्छेद किया गया। दर्शाइए कि
△ABE ∼ △CFB है।
हल:
दिया गया है कि E, समांतर चतुर्भुज ABCD की भुजा AD के बढ़ाव पर स्थित एक बिंदु है और BE, CD को F बिंदु पर प्रतिच्छेद करता है।
अब, △ABE और △CFB में:
∠A = ∠C (समांतर चतुर्भुज के विपरीत कोण समान होते हैं)
∠AEB = ∠CBF (AE ∥ BC होने के कारण परस्पर आंतर कोण – Alternate interior angles)
अतः AA समरूपता कसौटी के अनुसार:
∴ △ABE ~ △CFB
प्र.9: आकृति 6.39 में, ABC और AMP दो समरूप त्रिभुज हैं, जिनके कोण B और M समान हैं। सिद्ध कीजिए कि:
हल:
दिया गया है कि ΔABC और ΔAMP दो समकोण त्रिभुज हैं, जिनमें ∠B = ∠M = 90° हैं।
(i) ΔABC और ΔAMP में:
∠CAB = ∠MAP (सामान्य कोण – Common angle)
∠ABC = ∠AMP = 90° (प्रत्येक समकोण)
अतः, AA समरूपता कसौटी से:
∴ ΔABC ~ ΔAMP
(ii) चूँकि ΔABC ~ ΔAMP हैं,
तो समरूप त्रिभुजों में संगत भुजाएँ अनुपात में होती हैं:
अतः, CA/PA = BC/MP
इस प्रकार, कथन सिद्ध होता है।
प्र.10: दो त्रिभुज GH और EGF में:
∠ACB = ∠EGF तथा CD / GH = AC / FG दिया गया है। दर्शाइए कि:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
हल:
दिया गया है कि CD और GH क्रमशः ∠ACB और ∠EGF के समद्विभाजक (angle bisectors) हैं, जहाँ D और H बिंदु क्रमशः त्रिभुज ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं।
(i) प्रश्न में दिया गया है कि:
ΔABC ~ ΔFEG
∴ ∠A = ∠F, ∠B = ∠E, और ∠ACB = ∠FGE
चूंकि ∠ACB = ∠FGE, और CD तथा GH इन कोणों के समद्विभाजक हैं:
∴ ∠ACD = ∠FGH और ∠DCB = ∠HGE
अब, ΔACD और ΔFGH में:
∠A = ∠F (दी गई)
∠ACD = ∠FGH (कोण समद्विभाजक के कारण)
∴ ΔACD ~ ΔFGH (AA समानता मापदंड के आधार पर)
⇒ CD/GH = AC/FG
(ii) ΔDCB और ΔHGE में:
∠DCB = ∠HGE (ऊपर पहले ही सिद्ध किया गया)
∠B = ∠E (ΔABC ~ ΔFEG के कारण)
∴ ΔDCB ~ ΔHGE (AA similarity criterion)
(iii) ΔDCA और ΔHGF में:
∠ACD = ∠FGH (जैसा पहले सिद्ध हुआ)
∠A = ∠F (ΔABC ~ ΔFEG के कारण)
∴ ΔDCA ~ ΔHGF (AA similarity criterion)
प्र.11: आकृति 6.40 में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC को बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है, तो सिद्ध कीजिए कि △ABD ∼ △ECF।
हल:
प्रदत्त है कि ABC एक समद्विबाहु त्रिभुज है।
∴ AB = AC ✅
⇒ ∠ABD = ∠ECF ✅
अब त्रिभुज ΔABD और ΔECF में,
∠ADB = ∠EFC (प्रत्येक 90°) ✅
∠BAD = ∠CEF (पहले ही सिद्ध किया गया है) ✅
∴ ΔABD ∼ ΔECF (AA समरूपता कसौटी द्वारा) ✅
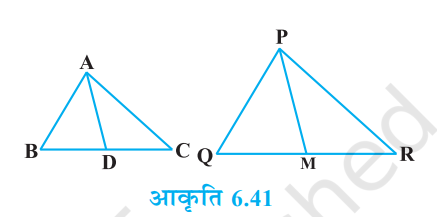
प्र.12: एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD, एक अन्य त्रिभुज PQR की क्रमशः भुजाएँ PQ और QR तथा माध्यिका PM के समानुपाती हैं। (आकृति 6.41 देखें) दर्शाइए कि △ABC ∼ △PQR।
हल:
दिया गया है कि त्रिभुज ABC और त्रिभुज PQR में,
AB/PQ = BC/QR = AD/PM ✅
जहाँ, D बिंदु BC का मध्यबिंदु है और M, QR का मध्यबिंदु है।
अतः AD और PM क्रमशः त्रिभुजों की माधिकाएँ हैं।
अब, त्रिभुज ABD और PQM पर विचार करते हैं:
AB/PQ = BD/QM = AD/PM (चूँकि D और M मध्यबिंदु हैं, इसलिए BD = BC/2 और QM = QR/2) ✅
∴ ΔABD ∼ ΔPQM (SSS समरूपता कसौटी द्वारा) ✅
∴ ∠ABD = ∠PQM (समरूप त्रिभुजों के संगत कोण) ✅
⇒ ∠ABC = ∠PQR (क्योंकि D और M मध्यबिंदु हैं, इसलिए पूरा कोण बराबर होगा) ✅
अब, त्रिभुज ABC और PQR में:
AB/PQ = BC/QR ………………………….(i)
∠ABC = ∠PQR ……………………………(ii)
∴ ΔABC ∼ ΔPQR (SAS समरूपता कसौटी द्वारा) ✅
अतः सिद्ध हुआ कि:
ΔABC ∼ ΔPQR ✅
प्र.13: एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA² = CB × CD।
हल:
दिया गया है कि ∠ADC = ∠BAC ✅
अब त्रिभुज ΔADC और ΔBAC में:
∠ADC = ∠BAC (प्रश्नानुसार) ✅
∠ACD = ∠BCA (साझा कोण) ✅
∴ ΔADC ∼ ΔBAC (AA समरूपता की कसौटी द्वारा) ✅
समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं:
CA / CB = CD / CA ✅
दोनों ओर CA से गुणा करें:
⇒ CA² = CB × CD ✅
अतः सिद्ध हुआ कि:
CA² = CB × CD ✅
प्र.14: एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA² = CB × CD।
हल:
दिया गया है कि ΔABC और ΔPQR दो त्रिभुज हैं, जिनमें AD और PM माधिकाएँ हैं तथा:
AB/PQ = AC/PR = AD/PM
पहले निर्माण करें: AD को E तक बढ़ाएँ जिससे कि AD = DE हो जाए। CE को जोड़ें।
इसी प्रकार, PM को N तक बढ़ाएँ जिससे कि PM = MN हो जाए। RN को जोड़ें।
अब, ΔABD और ΔCDE में:
AD = DE (निर्माण द्वारा)
BD = DC (क्योंकि D, BC का मध्यबिंदु है)
∠ADB = ∠CDE (विपरीत कोण)
∴ ΔABD ≅ ΔCDE (SAS सर्वांगसमता कसौटी द्वारा)
⇒ AB = CE (CPCT द्वारा) …………………………..(i)
अब, ΔPQM और ΔMNR में:
PM = MN (निर्माण द्वारा)
QM = MR (क्योंकि M, QR का मध्यबिंदु है)
∠PMQ = ∠NMR (विपरीत कोण)
∴ ΔPQM ≅ ΔMNR (SAS सर्वांगसमता द्वारा)
⇒ PQ = RN (CPCT द्वारा) ……………………………(ii)
अब, चूँकि AB/PQ = AC/PR = AD/PM (प्रश्नानुसार) और (i), (ii) से
⇒ CE/RN = AC/PR = AD/PM
⇒ CE/RN = AC/PR = 2AD / 2PM
⇒ CE/RN = AC/PR = AE / PN (क्योंकि AE = 2AD, PN = 2PM)
∴ ΔACE ∼ ΔPRN (SSS समरूपता कसौटी द्वारा)
⇒ ∠2 = ∠4 और ∠1 = ∠3
∴ ∠1 + ∠2 = ∠3 + ∠4 ⇒ ∠A = ∠P …………………(iii)
अब ΔABC और ΔPQR में:
AB/PQ = AC/PR (प्रश्नानुसार)
∠A = ∠P (सिद्ध हुआ)
∴ ΔABC ∼ ΔPQR (SAS समरूपता कसौटी द्वारा)
प्र.15: एक त्रिभुज ABC में ∠C = 90°, और D, AB पर एक बिंदु है, जो C से जोड़ने पर ∠D = ∠A होता है। सिद्ध कीजिए कि AC² = AD × AB।
हल:
लंबवत खंभे की ऊँचाई = 6 मीटर
खंभे की छाया = 4 मीटर
टॉवर की ऊँचाई = h मीटर
टॉवर की छाया = 28 मीटर
अब, ΔABC और ΔDEF में:
∠C = ∠E (सूर्य की किरणों द्वारा बना कोण)
∠B = ∠F = 90°
∴ ΔABC ∼ ΔDEF (AA समरूपता कसौटी द्वारा)
∴ AB/DF = BC/EF (समरूप त्रिभुजों की संगत भुजाओं का अनुपात)
⇒ 6/h = 4/28
⇒ h = (6 × 28) / 4
⇒ h = 168 / 4
⇒ h = 42 मीटर
अतः टॉवर की ऊँचाई = 42 मीटर
प्र.16: एक त्रिभुज ABC में, ∠C = 90° है और D, BC पर एक बिंदु है। यदि AC² = AD × AB सिद्ध करना हो, तो दर्शाइए कि ∠ACD = ∠BAD।
हल:
दिया गया है कि ΔABC ∼ ΔPQR
हमें ज्ञात है कि समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं।
∴ AB/PQ = AC/PR = BC/QR ……………………………(i)
तथा ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R …………………….(ii)
चूँकि AD और PM माधिकाएँ हैं, वे अपनी विपरीत भुजाओं को दो बराबर भागों में बाँटती हैं।
∴ BD = BC/2 तथा QM = QR/2 ………………………(iii)
समीकरण (i) और (iii) से,
AB/PQ = BD/QM ………………………………………(iv)
अब त्रिभुज ΔABD और ΔPQM में:
∠B = ∠Q (समीकरण ii से)
AB/PQ = BD/QM (समीकरण iv से)
∴ ΔABD ∼ ΔPQM (SAS समरूपता कसौटी द्वारा)
⇒ AB/PQ = BD/QM = AD/PM